Ir al contenido principal

DISTRIBUCIÓN BINOMIAL E HIPERGEOMÉTRICA

DISTRIBUCIÓN   BINOMIAL

Un experimento que queda descrito por una Distribución Binomial de probabilidad es aquel que posee las siguientes propiedades:
  • El experimento consiste en repetir "n" ensayos.
  • Cada ensayo da un resultado que puede ser clasificado como un éxito o un fracaso (de ahí el nombre, binomio).
  • La probabilidad de un éxito, denotada por "p", permanece constante a lo largo de las repeticiones del experimento.
El número de éxitos X=K en n-ensayos de un experimento binomial se llama una variable aleatoria binomial. La distribución de probabilidad de nuestra variable aleatoria X se llama Distribución Binomial de probabilidad y se expresa mediante la siguiente fórmula:

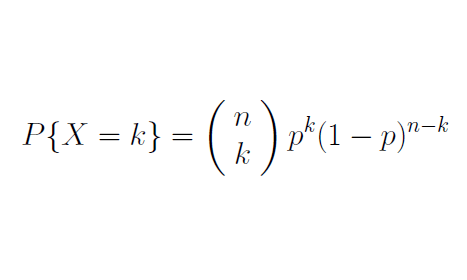
▷ Distribución binomial | Explicación y ejemplo
donde:
  • p k es la probabilidad de que nuestra variable aleatoria binomial sea igual a K, es decir, tengamos K éxitos.
  • p es la probabilidad de éxito de un solo ensayo
  • q=1-p es la probabilidad de fallo en un solo ensayo.
Ejercicios resueltos de distribucion binomial. Distribución ...

DISTRIBUCIÓN HIPERGEOMÉTRICA

Se emplea para calcular la probabilidad de obtener determinado número de éxitos en un espacio muestral de n ensayos; pero a diferencia de la distribución binomial es que los datos de la muestra se extraen sin reemplazo en una población finita población finita. Por esto es que el resultado de una observación depende o es afectado por el resultado de cualquier otra u otras observaciones anteriores.

La distribución hipergeométrica se emplea para muestreos sin reemplazo de una población finita cu ya probabilidad de ocurrencia cambia a lo largo del ensayo. 
Es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realizan experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial.

La distribución de probabilidad de la variable aleatoria hipergeométrica X, el número de éxitos en una muestra de tamaño n seleccionada de N posibles resultados, de los cuales k son considerados como éxitos y N − k como f racasos es:


Modelo Estadística


Ejemplo

Modelo Estadística


TABLA COMPARATIVA ENTRE LA DISTRIBUCIÓN BINOMIAL E HIPERGEOMÉTRICA





Comentarios

Publicar un comentario

Entradas populares de este blog

ESPERANZA MATEMÁTICA

Llamamos esperanza matemática (también conocida como esperanza, valor esperado, media poblacional o simplemente media) al número que expresa el valor medio de un fenómeno aleatorio. Denotamos la esperanza de una variable aleatoria X Para una variable aleatoria discreta con valores posibles  {\displaystyle x_{1},x_{2}\ldots x_{n}\,\!}  y sus probabilidades representadas por la función de la probabilidad   {\displaystyle p(x_{i})}  la esperanza se calcula como ejemplo: Si una tabla de mortalidad nos indica que en Estados Unidos una mujer de 50 años de edad puede esperar vivir 31 años más, esto no implica que cualquier persona en realidad espera que una mujer de 50 años de edad pueda cumplir 81 años y morir al día siguiente . D e modo similar, si leemos que en Estados Unidos una persona puede esperar comer 52 Kg de carne de res y beber 160  litros  de refresco por año o que un niño de un grupo de edad de 6 a 16 años puede esperar visitar ...
Publicar un comentario
Leer más

FORMAS DE REPRESENTAR GRÁFICAMENTE DISTRIBUCIONES DE PROBABILIDAD DE VARIABLES ALEATORIAS DISCRETAS

Función de distribución acumulada La función de distribución acumulada (CDF) calcula la probabilidad acumulada para un valor dado de x. Utilice la CDF para determinar la probabilidad de que una observación aleatoria que se tome de la población sea menor que o igual a cierto valor. También puede usar esta información para determinar la probabilidad de que una observación sea mayor que cierto valor o se encuentre entre dos valores. Para distribuciones discretas, la CDF proporciona la probabilidad acumulada para los valores de x que usted especifique. Probabilidad acumulada inversa Para un número p en el intervalo cerrado [0,1], la función de distribución acumulada inversa (ICDF) de una variable X aleatoria determina, donde sea posible, un valor de x tal que la probabilidad de X ≤ x sea mayor que o igual a p. La ICDF para distribuciones discretas La ICDF es más complicada para las distribuciones discretas que para las distribuciones continuas. Cuand...
Publicar un comentario
Leer más