DISTRIBUCIÓN NORMAL

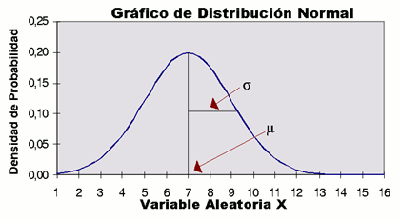
La distribución normal es , con mucho , la más importante de todas las distribuciones de probabilidad . Es una distribución de variable continua , con campo de variación. Fue descubierta por Gauss al estudiar la distribución de los errores en las observaciones astronómicas.

Debe su importancia a tres razones fundamentales:
Por un lado, un gran número de fenómenos reales se pueden modelizar con esta distribución (tales el caso de las características cuantitativas de casi todas las grandes poblaciones). Por otro lado, muchas de las distribuciones de uso frecuente tienden a aproximarse a la distribución normal bajo ciertas condiciones ; y , por último ,en virtud del Teorema Central del Limite, todas aquellas variables que puedan considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de observación) tienden a distribuirse con una distribución normal.

Propiedades

La forma de la curva de la distribución depende de sus dos parámetros: la media y la desviación estándar.

La media indica la posición de la campana, la gráfica se desplaza a lo largo del eje x.
A mayor desviación la curva será más "plana", dado que la distribución, en este caso, presenta una mayor variabilidad.
La curva es siimétrica respecto a la media.

Cuál es la fórmula para la distribución normal o curva de campana ...

Comentarios

Entradas populares de este blog

DISTRIBUCIÓN BINOMIAL E HIPERGEOMÉTRICA

DISTRIBUCIÓN BINOMIAL Un experimento que queda descrito por una Distribución Binomial de probabilidad es aquel que posee las siguientes propiedades: El experimento consiste en repetir "n" ensayos. Cada ensayo da un resultado que puede ser clasificado como un éxito o un fracaso (de ahí el nombre, binomio ). La probabilidad de un éxito, denotada por "p", permanece constante a lo largo de las repeticiones del experimento. El número de éxitos X=K en n-ensayos de un experimento binomial se llama una variable aleatoria binomial . La distribución de probabilidad de nuestra variable aleatoria X se llama Distribución Binomial de probabilidad y se expresa mediante la siguiente fórmula: donde: p k es la probabilidad de que nuestra variable aleatoria binomial sea igual a K, es decir, tengamos K éxitos. p es la probabilidad de éxito de un solo ensayo q=1-p es la probabilidad de fallo en un solo ensayo. ...

ESPERANZA MATEMÁTICA

Llamamos esperanza matemática (también conocida como esperanza, valor esperado, media poblacional o simplemente media) al número que expresa el valor medio de un fenómeno aleatorio. Denotamos la esperanza de una variable aleatoria X Para una variable aleatoria discreta con valores posibles {\displaystyle x_{1},x_{2}\ldots x_{n}\,\!} y sus probabilidades representadas por la función de la probabilidad {\displaystyle p(x_{i})} la esperanza se calcula como ejemplo: Si una tabla de mortalidad nos indica que en Estados Unidos una mujer de 50 años de edad puede esperar vivir 31 años más, esto no implica que cualquier persona en realidad espera que una mujer de 50 años de edad pueda cumplir 81 años y morir al día siguiente . D e modo similar, si leemos que en Estados Unidos una persona puede esperar comer 52 Kg de carne de res y beber 160 litros de refresco por año o que un niño de un grupo de edad de 6 a 16 años puede esperar visitar ...

FORMAS DE REPRESENTAR GRÁFICAMENTE DISTRIBUCIONES DE PROBABILIDAD DE VARIABLES ALEATORIAS DISCRETAS

Función de distribución acumulada La función de distribución acumulada (CDF) calcula la probabilidad acumulada para un valor dado de x. Utilice la CDF para determinar la probabilidad de que una observación aleatoria que se tome de la población sea menor que o igual a cierto valor. También puede usar esta información para determinar la probabilidad de que una observación sea mayor que cierto valor o se encuentre entre dos valores. Para distribuciones discretas, la CDF proporciona la probabilidad acumulada para los valores de x que usted especifique. Probabilidad acumulada inversa Para un número p en el intervalo cerrado [0,1], la función de distribución acumulada inversa (ICDF) de una variable X aleatoria determina, donde sea posible, un valor de x tal que la probabilidad de X ≤ x sea mayor que o igual a p. La ICDF para distribuciones discretas La ICDF es más complicada para las distribuciones discretas que para las distribuciones continuas. Cuand...

PROBABILIDAD Y ESTADÍSTICA

Buscar este blog